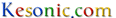突然发现对面坐著一个超甜美的MM迷你裙下修长匀称的双腿，要是能偷瞄到一点点……不知道该有多好……这样的情况应该是屡见不鲜了……

且让我们假设女孩双膝并隆的点和裙子上缘距离４公分，而裙摆到小裤裤之间的距离是１２公分，那么从侧面看来，目标区域和裙子就会形成一个直角三角形ａｂｃ。

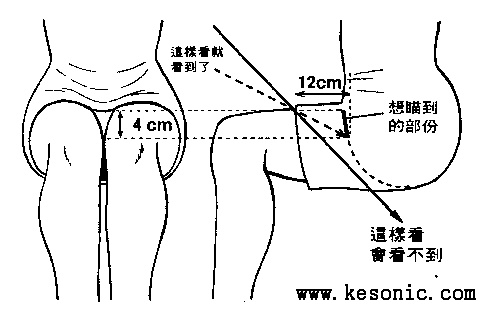
如果"观察者"的双眼ｅ正好在ｂｃ线段的延长线上，那么ｂ点就会落在他的视野内，如果我们做一条过ｅ并垂直於ａｃ线段延长线的直线ｄｅ的话，直角三角形ｄｅｃ就会和直角三角形ａｂｃ相似。

在△ａｂｃ中，ａｂ的长度是ａｃ的三分之一，因此在ａｂｃ里，ｄｅ的长度也应该是ｄｃ的三分之一，又因为ｄｃ是观察者的眼睛与裙子之间的水平距离，假设这个距离是１.６公尺，那么ｄｅ的长度（眼睛距离裙摆的高度）ｘ就是５３.３公分。不过一个身高１７０公分的观察者在采取普通坐姿时，他的眼睛与裙摆之间却会有７０公分的差距，换句话说.. 他必须要把头向下低个１７公分，而且为了达成这个目标，得要让屁股向前挺出４５公分才行。

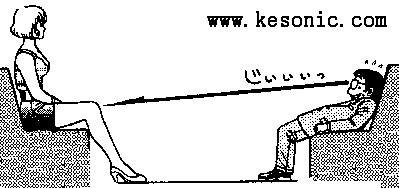
无论走到哪里，写字楼,百货公司……随时都会看到短裙美女上下楼梯的景象，看著白皙的双腿随著步伐不断交错，心里不禁暗想，要是我紧跟在她後面，一定有机会看到，跟在短裙美女後面爬楼梯会有好康，这是粉多人都有的迷思，不过，想一窥裙底机密也是有技巧的喔，短裙的内部状况大致就跟下图(内附一)所示一样：

一般"观察者"想看的地方，其实是半径１０公分的半球体部分，而裙子则与半球体相切并以向下１５公分的剪裁，巧妙地遮住了观察者的视线，从上图(附二)看来，直角三角形ｏｐｑ和ｏｒｑ是全等的。如果将ｑｒ线段（也就是观察者视线）延长并做出另一个直角三角形ｔｓｑ，那我们可由计算知道它的高是８.３公分，ｔｓｑ的高是底的０.４１５倍，所以，观察者如果想看到裙底风光，最低限度是让视线的仰角大於角ｔｑｓ，也就是高和底的比值要大於０.４１５倍。

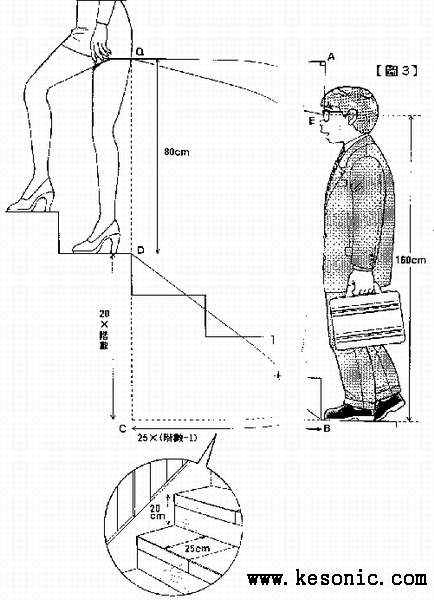
接下来，我们就要讨论△ａｅｑ的问题。假设观察者（身高１７０）眼睛的高度是１６０公分，而裙摆高度是８０公分，因为眼睛高度比裙摆高度大８０公分，所以裙摆与眼睛的高度差距（线段ａｅ），就比楼梯的高低差距(线段ｃｄ)小８０公分，因此直角三角型ａｅｑ的高和底可用以下两个式子来表示：

高：ａｅ＝２０×阶数－８０

底：ｑａ＝２５×（阶数－１）

高和底则须满足这个式子：ａｅ≧ｏａ×０.４１５

我们针对不同的阶梯差距列一张表：

│阶数│ １ │ ２ │ ３ │４│ ５ │ ６ ＞ │ ７ │ ８ │

│ａｅ│ -60 │ -40│ -20 │０│ 20 │ 40 │ ＞ 60 │ 80 │

│ｑａ│ ０ │ 25 │ 50 │75│ 100 │ 125 │ ＞ 150 │ 175 │

│比率│ ＊ │ -1.6 │ -0.4│０│ 0.2 │ 0.32│ ＞ 0.4 │0.457│

其中ａｅ是负值的情况，就表示裙摆问至还在眼睛下方，所以在阶梯差距小於４时，观察者是完全看不到裙子底下的。但是，当阶梯数增加到５或６的时候，喔喔~~~~就快看到啦！等到阶梯差到了８时，０.４１５的视奸障碍也就被破解啦！当然，这个差距愈大，视野也就愈宽广，不过可以看到的风光也会愈来愈小，这点请大家可别忘喽！